При разработке тома Электротехнические решения⎘ на этапе проектной документации наряду с выбором основного оборудования требуется рассчитать и выбрать ошиновку в его цепях.
На основе каких методик выполняются расчёты, каков их требуемый объём и что нужно брать за основу в качестве исходных данных — можно найти в этой статье.
Обращаем внимание, что отражённые здесь методики не актуальны для линий электропередачи, а применимы только для проводов и жёстких шин, а также опорных и подвесных изоляторов, на открытых и закрытых площадках подстанций и электростанций. Итак, начнём по порядку!
СОДЕРЖАНИЕ:
- Исходные параметры.
- Выбор ошиновки по длительно допустимому току.
- Проверка по экономической плотности тока.
- Расчёт максимального тяжения на фазу в нормальном режиме.
- Расчёт максимальной стрелы провеса.
- Проверка ошиновки на термическую стойкость.
- Проверка гибкой ошиновки на электродинамическое действие тока КЗ.
- Проверка расщеплённых проводов по взаимодействию между собой.
- Проверка жёсткой ошиновки на электродинамическое действие тока КЗ.
- Проверка опорной изоляции на электродинамическое действие тока КЗ.
- Проверка проводов по условиям короны.
1. Исходные параметры
Для выбора ошиновки нам понадобится:
- наибольший рабочий ток Iраб.max в рассматриваемой цепи.
Для проверки ошиновки следует знать (согласно п.4.1.3 ГОСТ Р 52736-2007⎘ и п.1.4.5 ПУЭ⎘):
- климатические параметры района, включая гололёдные условия и нормативные ветровые воздействия;
- монтажные таблицы стрел провеса проводов;
- тепловой импульс трёхфазного короткого замыкания Bк (на генераторном напряжении электростанций — трёхфазного или двухфазного, в зависимости от того, какой из них приводит к большему нагреву);
- двухфазный ток короткого замыкания I(2)кз.max — для проверки гибких проводников по условиям их допустимого сближения во время КЗ;
- ударный ток трёхфазного короткого замыкания iуд — для определения электродинамической стойкости жёстких шин и опорных конструкций.
По режиму короткого замыкания на станциях и подстанциях должны проверяться:
- гибкая и жёсткая ошиновка;
- опорные и несущие конструкции ошиновки;
- расстояния между распорками в расщеплённых фазах.
Исключения составляют:
- проводники, защищённые плавкими предохранителями с вставками на номинальный ток до 60 А, — по электродинамической стойкости;
- проводники, защищённые плавкими предохранителями независимо от их номинального тока и типа, — по термической стойкости;
- и прочее — см. гл.1.4 ПУЭ⎘.
Все расчёты выполним на реальных примерах, наиболее ярко отражающих тот или иной метод.
2. Выбор ошиновки по длительно допустимому току
Ещё раз напомним, что выбирать оборудование и ошиновку следует на основе параметров присоединённой линии или трансформатора.
Если длительно допустимый ток в линии 110 кВ
Iраб.max.ВЛ = 450 А
то выбираем в качестве ошиновки ячейки провод АС 240/39
Iдд = 610 А > Iраб.max.ВЛ = 450 А
В цепях силового трансформатора 63 МВА выберем провод АС 240/39 (на стороне 110 кВ) и четыре провода АС 500/64 (на стороне 6 кВ)
Iдд = 610 А > Iраб.max.T = 332 А
Iдд = 945∙4 = 3780 А > Iраб.max.T = 3031 А
Согласно выполненным расчётам ошиновка 110 и 6 кВ удовлетворяет требованиям по длительно допустимому току.
3. Проверка по экономической плотности тока
Согласно п.1.3.28 ПУЭ⎘ сборные шины электроустановок и ошиновка в пределах открытых и закрытых распределительных устройств всех напряжений проверке по экономической плотности тока не подлежат. Но необходимо проводить эту проверку для гибких токопроводов, соединяющих генератор с трансформатором в блоках электростанций.
\[ \mathrm{S = \frac{I}{J_{эк}}} \]
где I — расчётный ток в час максимума энергосистемы, А;
Jэк — нормированное значение экономической плотности тока, А/мм2, см. табл. 1.3.36 ПУЭ⎘.
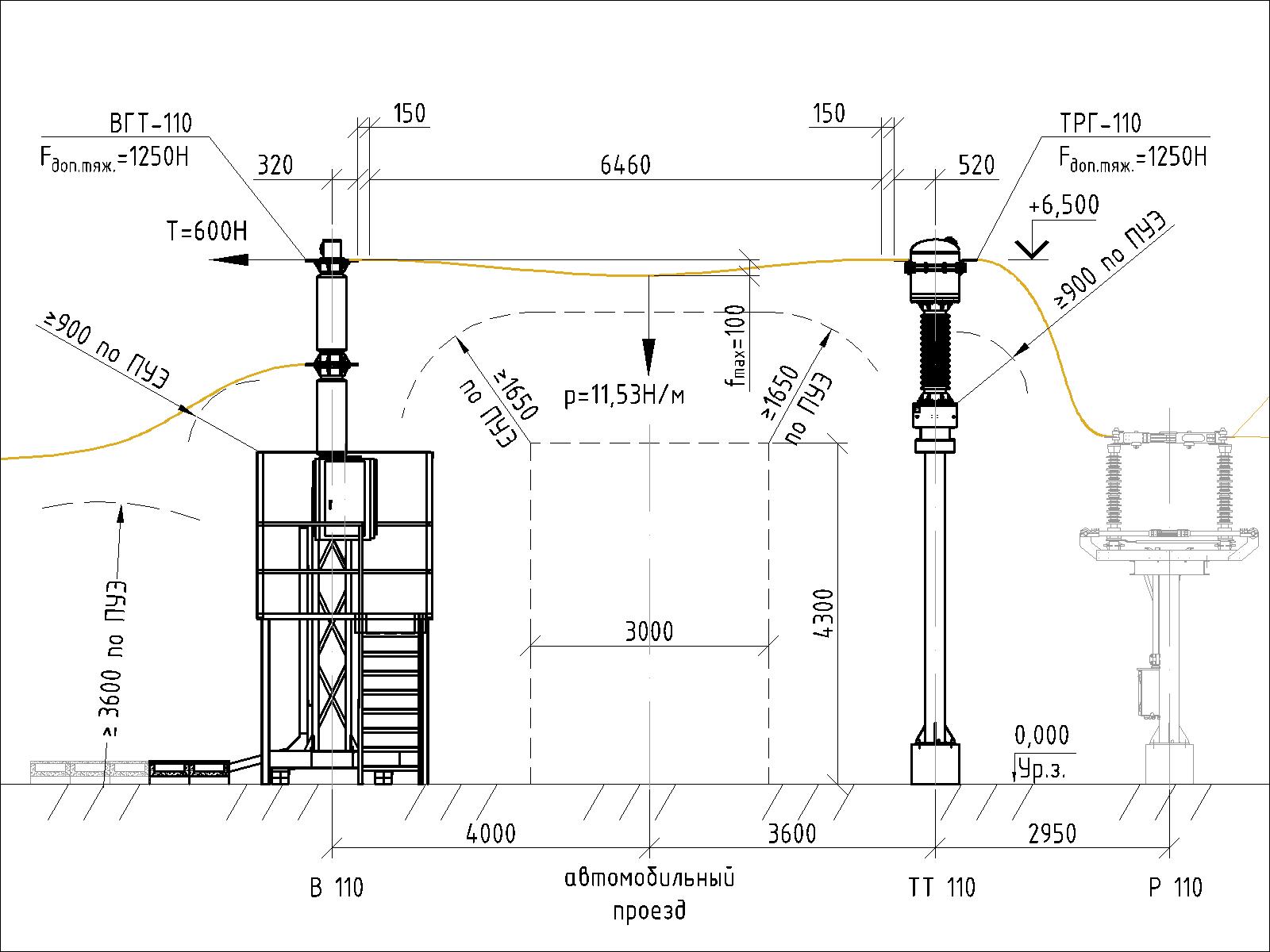
4. Расчёт максимального тяжения на фазу в нормальном режиме
Если для ошиновки трансформатора выбраны провода АС 240/39 (на стороне 110 кВ’) и 4хАС 500/64 (на стороне 6 кВ’’), то удельная нагрузка от собственного веса будет равна
p1 = mуд∙g [кг/м∙м/с2 = Н/м]
p1’ = 0,952∙9,8 = 9,33 Н/м
p1’’ = 4∙1,852∙9,8 = 72,6 Н/м
Удельная нагрузка от веса гололёда (по СП 20.13330⎘)
p2 = πbkμ(d + bkμ)ρg
где b — толщина стенки гололёда (учтём b = 5 мм для II района по гололёду);
k — коэффициент, учитывающий изменение толщины стенки гололёда по высоте;
d — диаметр провода;
μ — коэффициент, учитывающий изменение толщины стенки гололёда в зависимости от диаметра элемента кругового сечения;
ρ — плотность льда (принимаем 0,9 г/см3)
p2’ = 3,14∙5∙0,8∙0,8∙(21,6+5∙0,8∙0,8)∙0,9∙9,8∙10-3 = 2,198 Н/м
p2’’ = 4∙3,14∙5∙0,8∙0,8∙(30,6+5∙0,8∙0,8)∙0,9∙9,8∙10-3 = 2,995 Н/м
Удельная нагрузка от веса провода с гололёдом
p3 = p1 + p2
p3’ = 9,33 + 2,198 = 11,53 Н/м
p3’’ = 72,6 + 2,995 = 75,6 Н/м
Удельная нагрузка от давления ветра на провод без гололёда (по ПУЭ⎘)
p4 = αCxW0d
где α = 0,71 — коэффициент, учитывающий неравномерность ветрового давления;
Cx — аэродинамический коэффициент (1,1 — для проводов и тросов, свободных от гололеда, диаметром 20 мм и более; 1,2 — для всех проводов и тросов, покрытых гололёдом);
W0 — нормативное ветровое давление на высоте 10 м над поверхностью земли (учтём W0 = 230 Па для I района по ветру⎘)
p4’ = 0,71∙1,1∙230∙21,6∙10-3 = 3,88 Н/м
p4’’ = 4∙0,71∙1,1∙230∙30,6∙10-3 = 22 Н/м
Удельная нагрузка от давления ветра на провод с гололёдом (принимаем 0,25W0, α=1, Cx=1,2)
p5 = αCxW0(d+2b)
p5’ = 1∙1,2∙0,25∙230∙(21,6+2∙5)∙10-3 = 2,18 Н/м
p5’’ = 4∙1∙1,2∙0,25∙230∙(30,6+2∙5)∙10-3 = 11,21 Н/м
Удельная нагрузка от давления ветра и веса провода без гололёда
\[ \mathrm{p_6 = \sqrt{p_4^2 + p_1^2}} \]
p6’ = 10,1 Н/м
p6’’ = 75,85 Н/м
Удельная нагрузка от давления ветра и веса провода c гололёдом
\[ \mathrm{p_7 = \sqrt{p_5^2 + p_3^2}} \]
p7’ = 11,73 Н/м
p7’’ = 85,32 Н/м
Определим максимальное тяжение на фазу в наибольшем пролёте при наихудших внешних условиях
Tф.max = pmax∙L [Н/м ∙ м = Н]
где L — длина пролёта
Tф.max’ = 11,73∙6,5 = 76 Н
Tф.max’’ = 85,32∙3,3 = 282 Н
Максимальные итоговые значения сравниваются с допустимым тяжением на контактных выводах оборудования или шинодержателях шинных опор
Tф.max ≤ Fдоп.тяж
а значения удельных нагрузок понадобятся в дальнейших расчётах.
Для выключателей и трансформаторов тока 110 кВ выражение может иметь такой вид
Tф.max = 76 Н ≤ Fдоп.тяж = 1250 Н
а для шинных опор
Tф.max = 282 Н ≤ Fдоп.тяж = 1480 Н
5. Расчёт максимальной стрелы провеса
Стрелу провеса гибкого провода fmax в пролёте ОРУ можно рассчитать по следующей упрощённой формуле
\[ \mathrm{f_{max} = \frac{pL^2}{8T}} \]
где p = p3 — удельная нагрузка от веса провода с гололёдом, Н/м;
L — длина пролёта, м;
Т — тяжение провода, Н.
Тяжение провода на фазу в пролётах между порталами можно найти в монтажных таблицах (см. параметр Нг в типовом проекте 407-03-539⎘). Ввиду того, что пролёта длиной 7 метров в монтажных таблицах нет, обратим внимание на минимальное значение (1425 Н — для провода АС240/32 в пролёте 16 м, II район по гололёду). И помним, что максимальное тяжение не должно превышать допустимое тяжение на зажимах оборудования (1250 Н — у выключателя). Для нашего случая примем половину от последнего (600 Н). В случае подвеса двойного провода марки АС 500/64 это значение рекомендуют⎘ увеличивать до 981 Н.
Итого, максимальная стрела провеса провода над автомобильным проездом ОРУ 110 кВ
\[ \mathrm{f_{max} = \frac{11{,}53 \cdot 6{,}5^2}{8 \cdot 600} = 0{,}1\ м} \]
6. Проверка ошиновки на термическую стойкость
Проверка сечения ошиновки на термическую стойкость производится на основании известного теплового импульса трёхфазного короткого замыкания Bк
\[ \mathrm{q_{min} = \frac{\sqrt{B_к}}{C_т}} \]
где Cт — параметр, значение которого зависит от материала ошиновки (например, для сталеалюминевого провода Cт = 76, для жёстких шин Cт = 82, — см. табл. 7-9 ГОСТ Р 52736-2007⎘).
При токе КЗ на стороне 110 кВ, равным 42 кА, минимальное сечение
\[ \mathrm{q_{min} = \frac{\sqrt{158}}{76} \cdot 1000 = 165\ мм^2} \]
qАС240 = 275 > qmin
Сечение ошиновки превышает расчётные термические значения — требование термической стойкости соблюдается.
7. Проверка гибкой ошиновки на электродинамическое действие тока КЗ
Электродинамические силы взаимодействия F двух проводников при двухфазном КЗ I(2) следует определять по формуле
\[ \mathrm{F = \frac{2 \cdot 10^{-7} \cdot I^2 \cdot L \cdot K_ф}{a}} \]
где а — расстояние между фазами, м;
Кф — коэффициент формы проводника (по ГОСТ Р 52736⎘).
В пролётах ошиновки 110 кВ над автомобильным проездом и за трансформатором 63 МВА в режиме КЗ динамические силы будут равны
\[ \mathrm{F' = \frac{2 \cdot 36373^2 \cdot 6{,}5 \cdot 10^{-7}}{2} = 860\ Н} \]
\[ \mathrm{F'' = \frac{2 \cdot 25548^2 \cdot 3{,}3 \cdot 10^{-7}}{0{,}6} = 730\ Н} \]
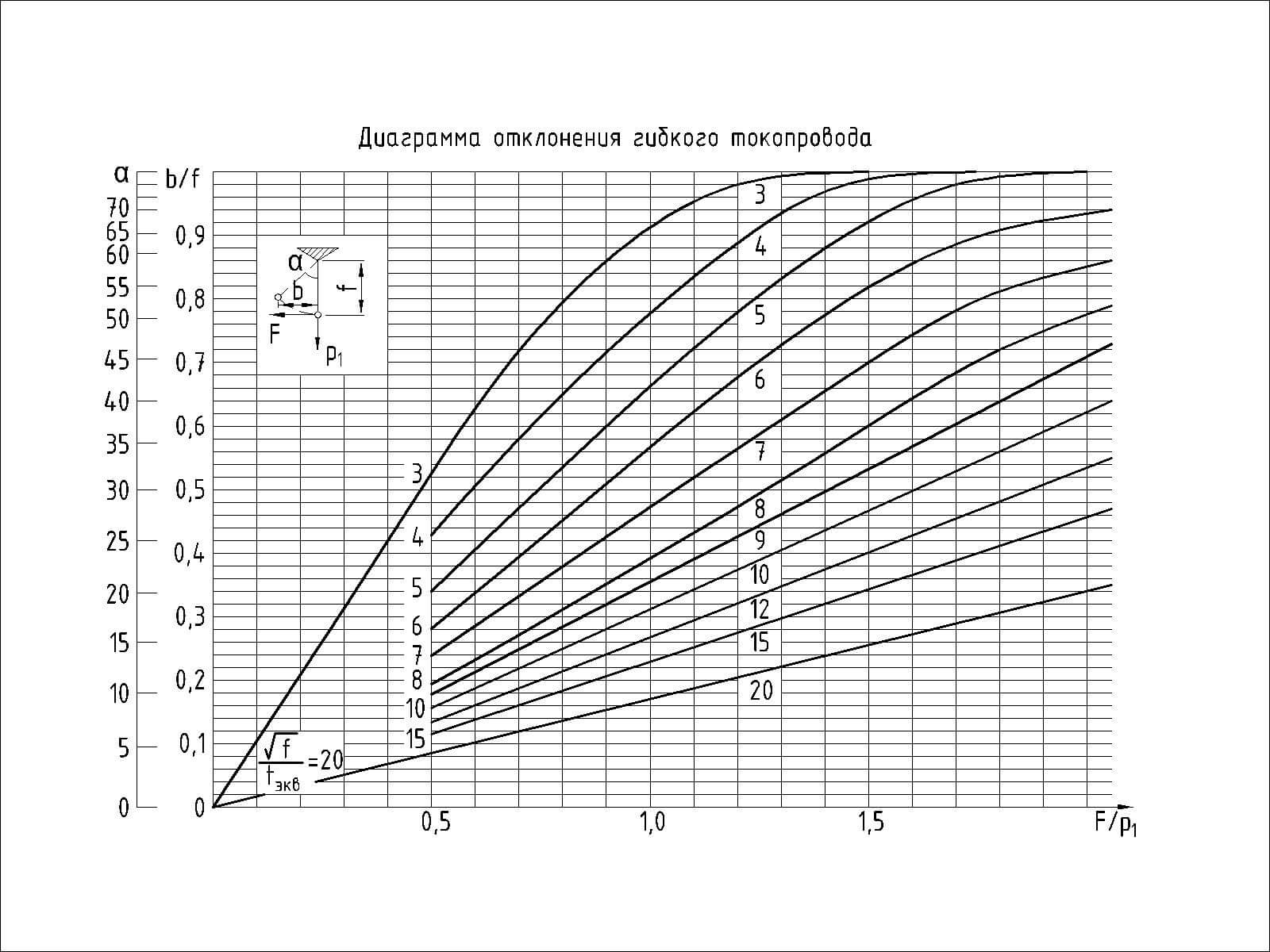
Получив данный результат и зная собственный вес проводов p1, для пролёта 110 кВ над проездом определим отношения
\[ \mathrm{\frac{\sqrt{f}}{t_{экв}} = \frac{\sqrt{0{,}1}}{0{,}06} = 5} \]
\[ \mathrm{\frac{F}{p_1} = \frac{860}{9{,}33} = 92} \]
за трансформатором на стороне 6 кВ
\[ \mathrm{\frac{\sqrt{f}}{t_{экв}} = \frac{\sqrt{0{,}12}}{0{,}06} = 6} \]
\[ \mathrm{\frac{F}{p_1} = \frac{730}{72{,}6} = 10} \]
где f — максимальная расчётная стрела провеса провода, м;
tэкв — эквивалентное время действия защиты, с.
По диаграмме отклонения b гибкого провода на основе полученных значений определяем его максимальное отклонение при КЗ.
Угол отклонения от вертикальной оси пролёта для ошиновки 110 кВ над проездом составит:
α = 90º (b=f)
для ошиновки 6 кВ за трансформатором
α = 90º (b=f)
Найденное значение b сравниваем с максимально допустимым:
\[ \mathrm{b_{доп}' = \frac{a - d - a_{доп}}{2} \ge b} \]
\[ \mathrm{b_{доп}' = \frac{2 - 0{,}0216 - 1}{2} = 0{,}49\ м > 0{,}1\ м} \]
\[ \mathrm{b_{доп}'' = \frac{0{,}6 - 0{,}15 - 0{,}22}{2} = 0{,}115\ м > 0{,}1\ м} \]
где a — расстояние между фазами, м;
d — диаметр фазы, м;
адоп — наименьшее допустимое расстояние между токоведущими частями разных фаз, м (по ПУЭ⎘).
Расчёты показали, что опасного сближения гибких проводов в результате динамического воздействия тока КЗ не произойдёт.
8. Проверка расщеплённых проводов по взаимодействию между собой
Рекомендуется проверять гибкие токопроводы с расщеплёнными фазами по электродинамическому взаимодействию проводников одной фазы — методику можно найти по ссылке⎘. Мы не будем транслировать здесь этот расчёт, так как к формулам имеются вопросы, а результат по их итогам может оказаться непредсказуемым. Данная методика требует доработки.
Расщеплённые провода фиксируются при помощи стандартных дистанционных распорок, которые рекомендуется устанавливать через каждые 5-6 метров, но как минимум одну — на перемычку.
9. Проверка жёсткой ошиновки на электродинамическое действие тока КЗ
Определим силу взаимодействия между жёсткими шинами на стороне генераторного напряжения 6 кВ в блоке «генератор-трансформатор».
Максимальная сила, возникающая при трёхфазном коротком замыкании, будет равна
\[ \mathrm{F_{max} = \frac{\sqrt{3} \cdot 10^{-7} \cdot l \cdot i_{уд}^2 \cdot K_ф \cdot K_{расп}}{a} = \frac{\sqrt{3} \cdot 10^{-7} \cdot 1 \cdot 289000^2 \cdot 0{,}2 \cdot 1}{1} = 2893\ Н} \]
где а — расстояние между фазами, м;
Кф — коэффициент формы (равен 0,2 — по ГОСТ Р 52736⎘);
Красп — коэффициент, зависящий от взаимного расположения проводников (для проводников, расположенных в одной плоскости, равен 1).
Максимальное напряжение в материале шины σmax определим по формуле
\[ \mathrm{\sigma_{max} = \frac{F_{max} \cdot l}{\lambda \cdot W} = \frac{2893 \cdot 1}{8 \cdot 0{,}000048} = 7{,}5\ МПа} \]
где λ — коэффициент, зависящий от условия опирания шин (равен 8 для простых опор);
W — момент сопротивления поперечного сечения шины (по ГОСТ Р 52736⎘)
\[ \mathrm{W = \frac{bh^2}{3} = \frac{0{,}01 \cdot 0{,}12^2}{3} = 0{,}000048\ м^3} \]
Допустимое напряжение в материале жёстких шин следует принимать равным 70 % временного сопротивления разрыву материала шин σр
σдоп = 0,7∙σр = 0,7∙89 = 62 МПа
где σр для алюминиевого сплава АД31Т равно 89 МПа, для меди — 175 МПа.
Условие
σmax < σдоп
соблюдается — шины выдержат ударный ток короткого замыкания.
10. Проверка опорной изоляции на электродинамическое действие тока КЗ
Допустимую нагрузку на изгиб или растяжение (сжатие) опорного изолятора Fдоп.изг следует принимать равным 60 % суммарного разрушающего усилия Fразр.изг
Fдоп.изг = 0,6∙Fразр.изг = 0,6∙10 = 6 кН
где Fразр.изг для изолятора ОСК-10-110 равно 10 кН.
Условие
Fmax = 2,9 кН < Fдоп.изг = 6 кН
соблюдается.
При расчётах важно учитывать конструкцию самих опор и способ крепления с учётом смещения опасного сечения — методика подробно описана в ГОСТ Р 52736⎘ и РД 153-34.0-20.527⎘.
11. Проверка проводов по условиям короны
Проверка по условиям короны необходима для гибких проводников при напряжении 35 кВ и выше.
Разряд в виде короны возникает при максимальном значении начальной критической напряжённости электрического поля
\[ \mathrm{E_0 = 30{,}3 \cdot m \cdot \left(1 + \frac{0{,}299}{\sqrt{r_0}}\right) = 30{,}3 \cdot 0{,}82 \cdot \left(1 + \frac{0{,}299}{\sqrt{1{,}1}}\right) = 31{,}9\ кВ/см} \]
где m — коэффициент, учитывающий шероховатость поверхности провода (для многопроволочных проводов m = 0,82);
r0 — радиус провода, см.
Максимальное значение напряжённости электрического поля вокруг провода определяется по формуле
\[ \mathrm{E = \frac{0{,}354 \cdot U}{r_0 \cdot \lg\left(\frac{a}{r_0}\right)} = \frac{0{,}354 \cdot 110}{1{,}1 \cdot \lg\left(\frac{250}{1{,}1}\right)} = 15\ кВ/см} \]
где а — расстояние между соседними фазами, см.
При горизонтальном расположении проводов напряжённость на среднем проводе примерно на 7% больше величин, определённых по формуле. Провода не будут коронировать, если наибольшая напряжённость поля у поверхности любого провода не более 0,9Е0. Таким образом, условие отсутствия короны можно записать в виде
1,07Е ≤ 0,9Е0
16 < 28,7
Согласно расчётам, на проводах 110 кВ корона отсутствует.
Минимальный диаметр проводов по условию короны и радиопомех, для разных классов напряжения, также можно найти в справочнике⎘.
ВЫВОД
Все правила, отражённые в этой статье, актуальны и применимы для большинства объектов энергетической отрасли, но многие вопросы ещё требуют доработки на законодательном уровне. Некоторые методики требуют изменений, в том числе, потому что единицы не приведены к международной системе СИ. А часть данных, таких как монтажные стрелы провеса, просто не сформирована.
ССЫЛОЧНАЯ ЛИТЕРАТУРА
Более подробную информацию можно найти в ГОСТах, стандартах организаций и справочниках. Все указанные нормативно-технические документы, в актуальных редакциях, хранятся на странице НТД и отфильтрованы по ссылке⎘.
